Bon j'ai bossé tard hier soir pour vous concocter qq images sympa

.
Résumé de l'épisode précédent :
Comme cela a été remarqué très justement par Cat01, la justification de l'utilité de l'interpolation à une réso supérieure (upscaling) de n'importe quelle image digitale repose sur l'hypothèse qu'on ne cherche pas à représenter des fréquences spatiales supérieure à une limite donnée (en gros celle qui donne une alternance pixel blanc-pixel noir une fois échantillonnée). Dans ce cas, l'upsaling joue le rôle d'un filtre analogique qui permet de représenter avec plus de points les hautes fréquences présentes dans l'image.
On peut alors se poser une nouvelle question : est-ce que interpolation et représentation de transitions "nettes" font bon ménage ?
La réponse est oui sans hésitation pour les raisons suivantes :
1. Qui dit transition nette dit (très) haute fréquence spatiale qui sauf cas particulier va être filtrées par l'échantillonnage et la compression mpeg2. Il n'existe donc pas de transitions véritablement nettes dans un signal vidéo compressé. Le cas particulier correspond à une transition qui s'aligne partifaitement en horizontale ou verticale sur les pixels de la matrice (cf. point 2).
2. Lorsqu'on filme une transition nette, à moins d'un coup de bol incroyable, il y aura toujours des pixels de la matrice CCD à cheval sur les zones claires et sombres de la transition. Ces pixels vont donc intégrer une luminosité moyenne et resortir gris. Donc en pratique, les transitions nettes n'existent que dans les mires créées avec un PC

.
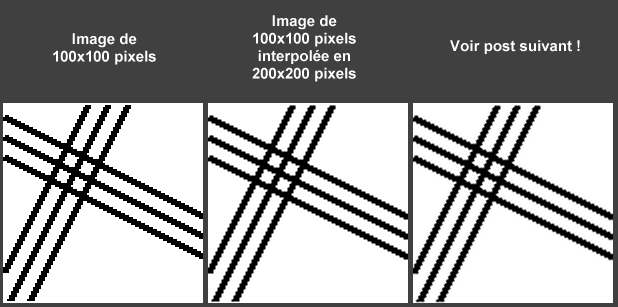
3. On pourrait croire qu'une image non interpolée à plus de chance de mieux représenter une transition nette car le contraste entre deux pixels successifs de part et d'autre de la transition sera supérieur. C'est vrai uniqt si la transition passe du noir au blanc sur un pixel ce qui est très improbable à cause des 2 points précédents (cf. série du haut sur la 1ère image attachée à ce post). Par contre, dès que la transition se fait sur au moins 2 pixels, ce n'est plus vrai. Ceci est simplement dû au fait que l'image interpolée possède plus de pixels, mais que ces pixels sont PLUS PETITS. Par conséquent, la transition occupe toujours le même espace sur l'écran (ce point n'est tout à faire exact car il y a tjrs un effet de bord lorsqu'on passe un filtre spatial matriciel) et le contraste entre 2 points séparés par la même distance de part et d'autre de la transition reste quasiment identique (cf. série du bas).
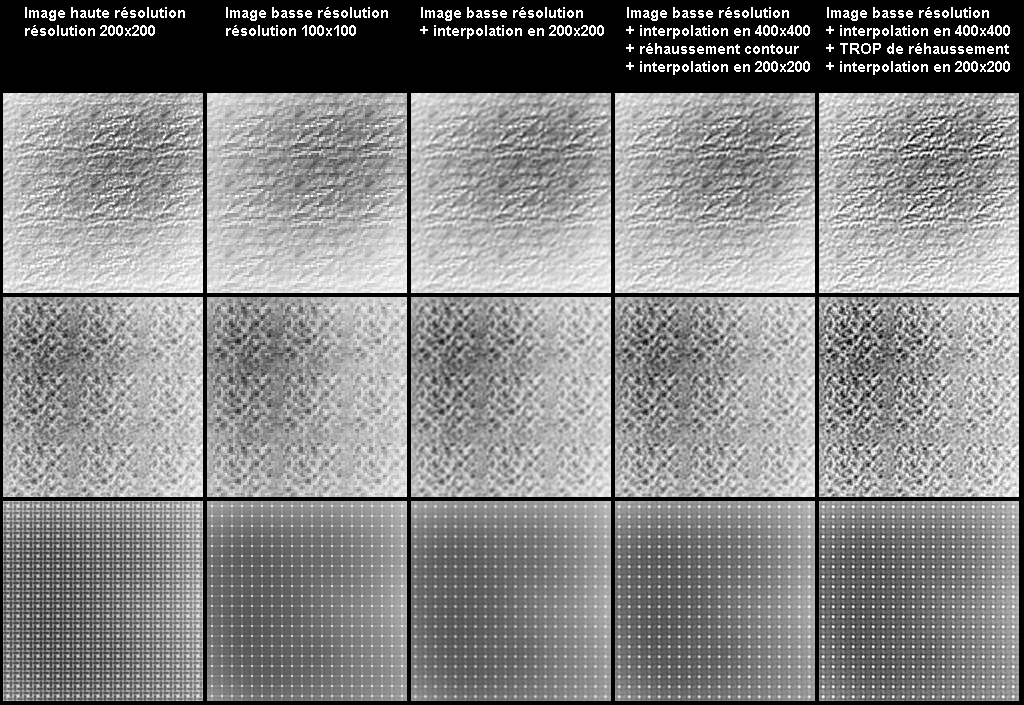
4. S'il s'avère que la transition "nette" n'est pas totalement parallèle à la matrice du projo (cas plutôt fréquent), il va y avoir échantillonnage spatial et risque de voir apparaître des effets d'escaliers disgratieux que l'oeil repère immédiatement... et interprète à juste titre comme un manque de résolution. L'interpolation permet de lisser ces effets d'escalier (antialiasing) et l'expérience montre que l'oeil préfère nettement ce type d'image qu'il juge plus "naturelle" (ou moins "pixélisée") : cf. la 2e image.
4 bis. Lorsqu'on projette sur un écran une image de taille 800x600 et la même image interpolée en 1600x1200, on a vu que l'image interpolée possède des pixels bcp plus petits. Là où il y avait avant un pixel, il y en a maintenant 4. Par conséquent, la transition occupe toujours le même "espace" sur l'écran mais perd son aspect pixelisée (on retrouve l'effet de filtre). Là encore, il s'avère que l'oeil préfère nettement ce type de rendu : cf. les transitions sur les bords des pétales (transition sur 2 pixels) dans la 3ème image.