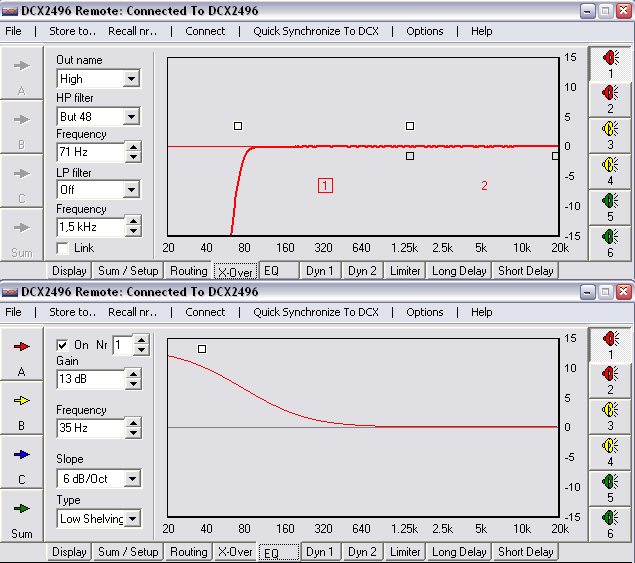
Elle permet de transformer toute réponse du 2nd ordre de Fs et Qs donnés en une autre réponse du 2nd ordre de Ft et Qt souhaités.
Tout HP dans une enceinte close ayant une réponse passe haut du 2nd ordre [note 2], la transforme de Linkwitz permet par exemple
d'étendre la réponse dans les basses d'un boomer ou de transformer la réponse basse d'un médium ou même d'un tweeter pour la rendre plus compatible avec le filtrage prévu
Le DCX2496 ne possède pas hélas la fonction d'égalisation "transformé de Linkwitz" , aussi j'ai essayé de trouver comment la remplacer avec les fonctions de filtrage disponibles.
C'est possible, bien que pas vraiment simple. Voici le résultat de mes cogitations. Je ne prétend pas que ce qui suit soit original (d'autres ont bien du y penser avant) , mais j'espère que ca pourra servir à quelqu'un.
Un peu (beaucoup?) de théorie
Note : pour ceux qui sont allergique aux formules, allez directement au chapitre "la solution"
La fonction de transfert de la "transforme de Linkwitz" est :
LT(s)=(s²+ws/Qs*s+ws²)/(s²+wt/Qt*s+wt²)
avec ws=2*π*Fs et wt=2*π*Ft
C'est très malin : cette fonction de transfert possède 2 zéros qui annulent les pôles de la réponse du 2nd ordre d'origine et les remplace par ses propres pôles. Simple mais il fallait y penser.
De son côté, le DCX possède 2 fonctions d'égalisation qui vont nous servir : le "LP" et le "BP"
Filtre LP
C'est un « Low Pass shelving filter» à la sauce Behringer.
Il possède 3 paramètres :
- Fréquence centrale : Fo,
- Gain : Go
- Pente : 6 ou 12 db/o
Seul la version à pente de 12db/o va nous intéresser.
Après quelques tâtonnements (et erreurs cf note 1), il apparait que sa fonction de transfert est différente suivant que le gain
Go est positif ou négatif

- Si Go < 0
Alors la fonction de transfert est donnée par :
LPL(s)=(s²+wo/Q*s+wo²)/(s²+wo/Q/A*s+wo²/A²)
avec : wo=2*π*Fo , A=10^(Go/40) et Q=0.707
Si on regarde bien, la fonction LP ressemble un peu à celle de la transformé de Linkwitz LT.
En fait pour qu'elles soient identiques (je vous passe les calculs) il faut que :
1) Fo=Fs
2) A=Fs/Ft avec Go=40*log(Fs/Ft)
3) Qs=Q
4) Qt=Q
Les deux premières égalités permettent de calculer les paramètres du filtre en fonction de Fs et Ft.
Les deux suivantes sont des mauvaises nouvelles : elles nous indiquent qu'on ne peut utiliser ce filtre LP en tant que transformé de Linkwitz, que si Qs=Qt=Q=0.707.
En fait, le filtre, va permettre de transformer toute réponse du 2nd ordre de fréquence Fs et Qs=0.707 en une réponse du 2nd ordre de fréquence Ft et Qt=0.707.
A noter que Go>0 => A > 1 et donc tout ceci n'est valide que si Fs>Ft. - Si Go > 0
Alors la fonction de transfert est donnée par :
LPH(s)=(s²+A*wo/Q*s+wo²*A²)/(s²+wo/Q*s+wo²)
avec toujours : wo=2*π*Fo , A=10^(Go/40) et Q=0.707
Là encore, la fonction LPH ressemble un peu à celle de la transformé de Linkwitz LT.
Pour qu'elles soient égales, il faut que :
1) Fo=Ft
2) A=Fs/Ft avec Go=40*log(Fs/Ft)
3) Qs=Q
4) Qt=Q
Ce sont les même conditions que dans le cas Go<0 sauf pour Fo égal ici à Ft et non pas Fs.
Et donc,là encore,le filtre, va permettre de transformer toute réponse du 2nd ordre de fréquence Fs et Qs=0.707 en une réponse du 2nd ordre de fréquence Ft et Qt=0.707.
Mais Go<0 => A < 1 et donc Fs<Ft
En conclusion le filtre LP du DCX2496, permet bien d’effectuer une transformé de Linkwitz uniquement si les réponses source et cible ont un Q=0.707.
Si ce n'est pas le cas un autre type de filtre va nous être utile :
Filtre BP
Il possède 3 paramètres :
- Fréquence centrale : Fo
- Gain : Go
- facteur qualité : Qo
Là aussi, Il apparait que sa fonction de transfert est différente suivant le signe du gain :
- Si Go > 0
Alors la fonction de transfert est donnée par :
PB(s)=(s²+A*wo/Qo*s+wo²)/(s²+wo/Qo*s+wo²)
avec : wo=2*π*Fo , A=10^(Go/20)
Si on veut l'utiliser comme transformé de Linkwitz, il faut que :
1) Fo=Fs=Ft
3) Qo=Qt
2) A=Qt/Qs cad Go=20*log(Qt/Qs)
La 1ère nous indique qu'on ne pourra utiliser ce filtre que pour changer le facteur de qualité et pas la fréquence.
Les deux autres nous indiquent comment calculer les paramètres du filtre. - Si Go < 0
Alors la fonction de transfert est donnée par :
PB(s)=(s²+wo/Qo*s+wo²)/(s²+wo/Qo/A*s+wo²)
Si on veut l'utiliser comme transformé de Linkwitz, il faut que :
1) Fo=Fs=Ft
2) Qo=Qs
3) A=Qt/Qs cad Go=20*log(Qt/Qs)
Là encore, la 1ère nous indique qu'on ne pourra utiliser ce filtre que pour changer le facteur de qualité et pas la fréquence,
et les deux autres nous indiquent comment calculer les paramètres du filtre.
Ce sont les même condition que pour G>0 sauf Qo égal ici à Qs et non Qt
La solution
Comme on peut le voir, aucun des 2 types de filtre ne permet d'implémenter une transformé de Linkwitz de façon
générale . Il y a toujours des contraintes.
Alors comment faire ?
Et bien il suffit de combiner les 2 types de filtre de la façon suivante :
1) Un 1er BP
Ce 1er filtre va juste modifier le facteur de qualité de la réponse de départ (Qs) de façon à l'amener à un Q=0.707.
Les paramètres de ce filtres sont :
Fo=Fs , Go=20*log(Q/Qs)
Si Qs>Q
Qo=Qs
sinon
Qo=Q
Si Qs=Q=0.707 alors ce filtre est inutile.
2) un filtre LP
Combiné avec le 1er, ce filtre va permettre d'arriver à une réponse caractérisée par Ft,Q=0.707.
Les paramètres de ce filtres sont :
Go=40*log(Fs/Ft)
Si Fs<Ft alors
Fo=Fs
sinon :
Fo=Ft
Si le Qt désiré était égal à Q=0.707 alors ont s'arrête là
sinon il faut appliquer un 3eme filtre :
3) Un 2ème filtre BP
Ce filtre va modifier le facteur de qualité de façon à avoir le Qt voulu.
Les paramètres de ce filtres sont :
Fo=Ft
Go=20*log(Qt/Q)
Si Qt>Q
Qo=Qt
sinon
Qo=Q
Et voila !
La combinaison des 3 , va bien nous donner un fonction de transfert correspondant à la transformé de Linkwitz !
Il faut, dans le pire des cas, 3 filtres pour en simuler 1, dommage que le DCX n'ait pas cette fonction nativement .....
Conclusion
On peut simuler une transformé de Linkwitz avec le DCX2496 en utilisant une combinaison de filtre LP et BP, mais c'est pas vraiment simple.
Quoiqu'il en soit, tout cela m'aura permit de mieux connaitre les caractéristiques des filtres du DCX et comment les utiliser.
Note 1: Des 1ères versions de ce texte comprenaient des formules erronées pour les filtres et donc pour les formules à appliquer en conclusion. Tout cela à été corrigé le 7/05/2016.
Note 2 : On peut faire la même chose pour un passe bas du 2nd ordre, il sufit d'utiliser un HP au lieu d'un LP, en inversant Ft et Fs dans le calculs du filtre