sax.tenor a écrit:
Bonjour,
quelqu'un pourrait-il me guider pour le calcul de la longueur (pas de l'aire) du tracé d'une spirale d'Archimède (un sillon de disque)? C'est -sauf erreur- un calcul intégral. J'ai quitté tout cela il a fort longtemps… J'ai repris pour mon plaisir et pour ne pas sécher en soutien scolaire en maths et sciences, heureusement d'un niveau limité à la 3ème et 2nde.
Sinon, je procéderai par approximation avec une série de cercles de rayon en progression arithmétique. Ca, je sais (encore) faire malgré les années qui passent.
Merci
Edit le 20 avril avec la solution :
Le plus simple était de contacter mon frangin (MERCI à lui), pas rouillé du tout
 , et ravi de rajeunir de xx années
, et ravi de rajeunir de xx années  . Il s'agit bien d'une intégrale ∫ .
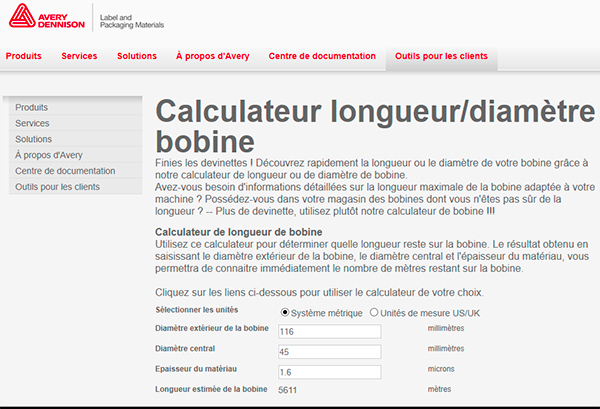
. Il s'agit bien d'une intégrale ∫ .Ma gêne était (partiellement) due à la superposition de deux notions sous le même nom: le "pas" A d'une spirale que j'exprime en mm ; ce qui est la progression du rayon pour chaque rotation (2 PI radian), et le pas angulaire a qu'on exprime en mm/rd (radian) qui est la même valeur rapportée au radian
a = A / 2 PI
Une spirale d'Archimède est caractérisée par r = a x Theta
La longueur de la spirale est L = ∫ dl entre les bornes 1 et 2 (rayon mini et rayon maxi)
Pour un pas angulaire de a, on a d (THETA) = d r / a Il vient : L = ∫ r x dr / a entre les rayons mini r1 et maxi r2
Ce qui donne (ce n'est vraiment pas compliqué pour celui "qui est passé par là") : L = (r2xr2 - r1xr1) / 2a
Cas particulier : la spirale est un cercle; a = cste et dans ce cas, l'intégrale de la "longueur" devient L = 2 PI r C'est pas beau les maths ?
Ce qui est jouissif est que mon approximation d'une suite de cercles concentriques "matches" à 100,0 % du fait que le pas de la spirale est faible rapporté aux diamètres.
Je me suis amusé à multiplier le pas de la spirale par 1000 et j'ai comparé les deux résultats qui ne diffèrent que 4 %.
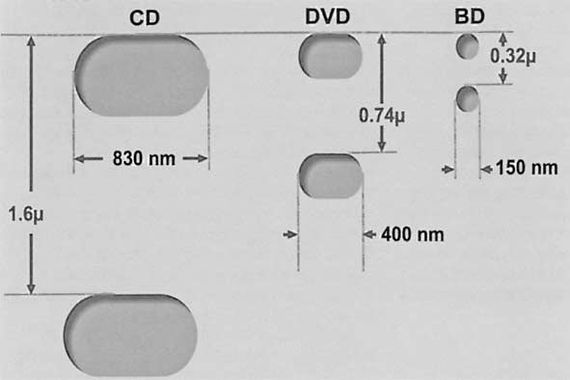
Pour les "forcenés", j'ai calculé le "trajet" disponible pour graver 16 kHz sur un 33 tours. Je garde mes CD.
Calculs à votre disposition.