Dans la documentation JBL du lien indiqué par JIM, figure à la fin du PDF la
formule de Peutz permettant d’estimer la
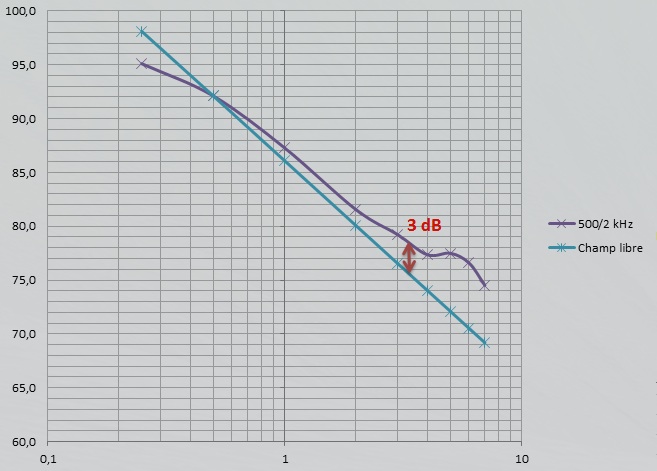
pente de l’asymptote du niveau de pression du champ diffus c'est-à-dire bien au-delà de la distance critique. Cette relation n’est valide que lorsque la hauteur sous plafond est bien plus petite que les autres dimensions de la salle.
pente selon Peutz =0,4√V/(H.Tr)où
V est le volume de la salle
H hauteur de la salle
Tr temps de réverbération
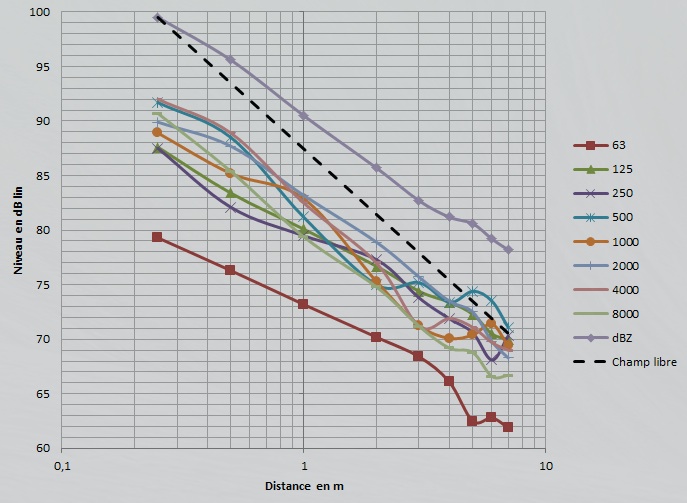
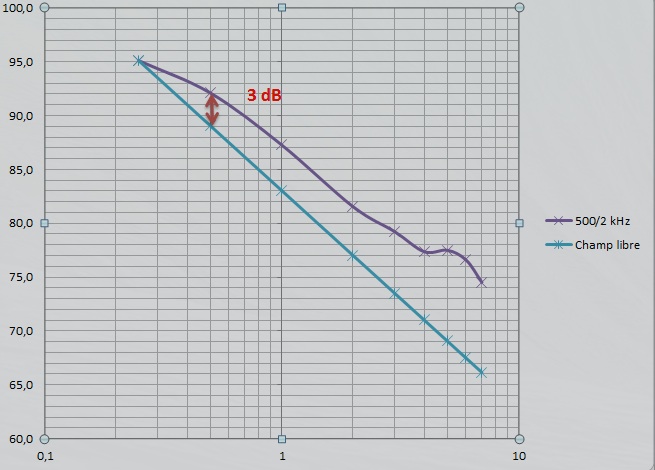
D’ordinaire, on admet dans le formalisme de Sabine que cette asymptote est horizontale, mais en pratique le niveau continu à décroître même en plein champ diffus comme le montre le graphique ci-dessous relatif aux mesurages réalisés dans un gymnase (distance critique=1 m environ).
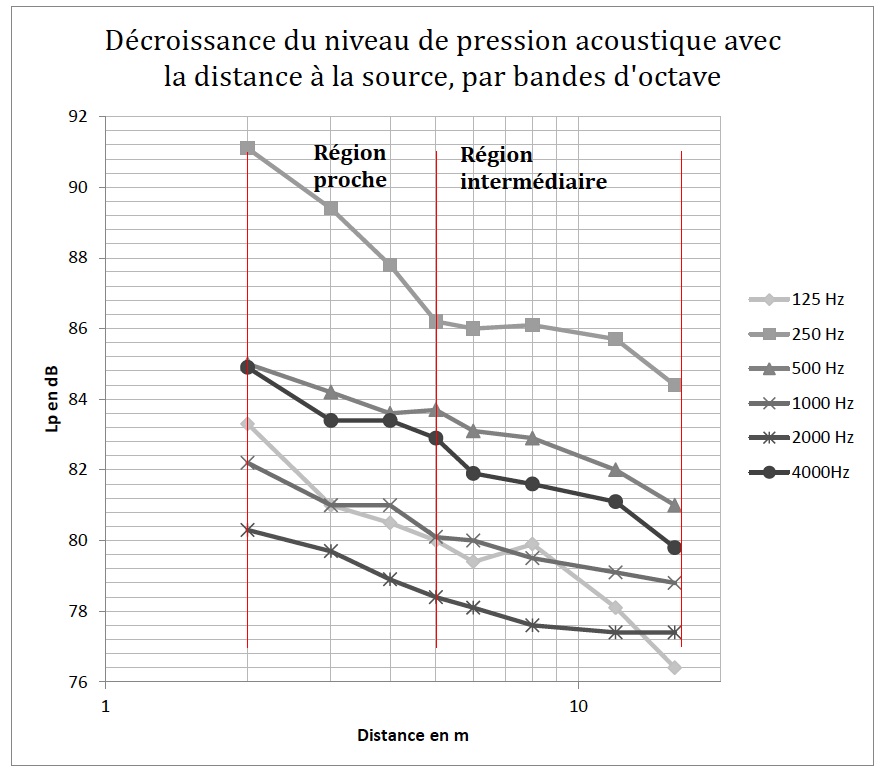
Je n’ai jamais eu l’occasion de comparer cette pente théorique selon la relation empirique de Peutz, avec la décroissance mesurée in situ.
La décroissance du niveau de pression est indiquée ci-dessous à travers l’indicateur DL2 ( taux de décroissance par doublement de la distance) qui n’est autre que la pente de la droite de régression par la méthode des moindres carrées, dans la zone dite intermédiaire, au delà de 5 m selon la norme ISO 14257 et qui indique par un indice unique, comme souvent en acoustique, une estimation de la décroissance du son.

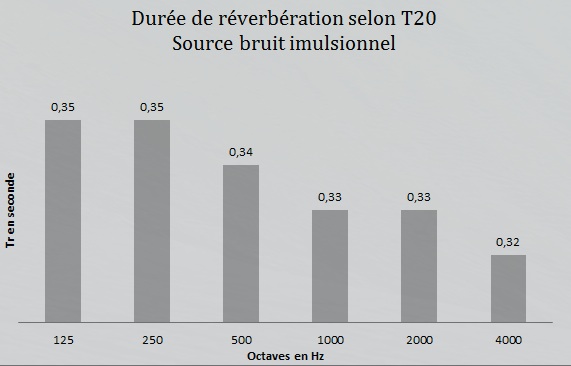
Les valeurs calculées à l’aide de la formule de Peutz donne des résultats assez disparates selon les octaves. Toutefois, les dimensions du local sont 19,8 x 9,0 x 4,2 m et si la longueur est bien plus grande que la hauteur de la salle ce n’est plus le cas pour la largeur ! Le gymnase ne se prête pas trop à la formule de Peutz.
On est bien loin de considération homecinephile mais c'est en relation directe avec la distance critique et cela me permet de laisser aussi une trace sur la toile sur un sujet assez peu abordé même dans la littérature acoustique:wink:



Bachi

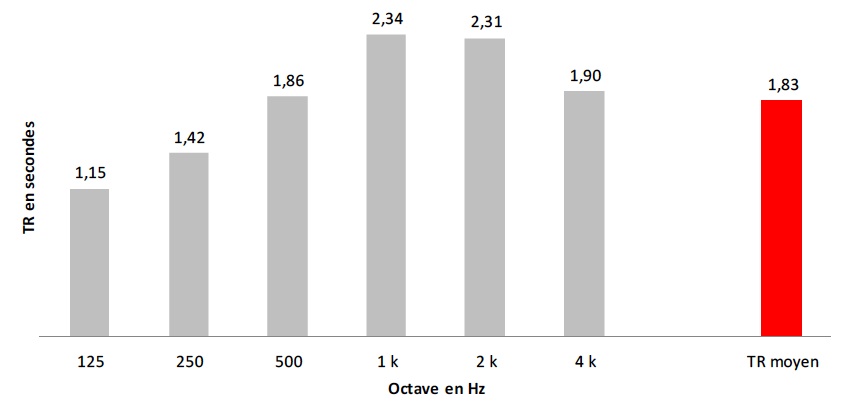






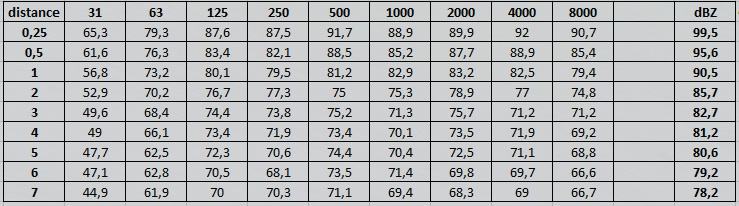
 C'est étrange ! Maintenant, mes mesures en champ proche sont entachées d'incertitudes importantes en raison des interférences entre le boomer et la compression. J'ai opté pour une mesure dans l'axe du pavillon. Ça, ajouté à l'incertitude sur l'origine, ça commence à faire beaucoup, même pour de la métrologie domestique
C'est étrange ! Maintenant, mes mesures en champ proche sont entachées d'incertitudes importantes en raison des interférences entre le boomer et la compression. J'ai opté pour une mesure dans l'axe du pavillon. Ça, ajouté à l'incertitude sur l'origine, ça commence à faire beaucoup, même pour de la métrologie domestique