|
|
Modérateurs: Modération Forum Installations, Modération Forum Haute-Fidélité, Modération Forum Univers Casques, Le CA de l’Association HCFR • Utilisateurs parcourant ce forum: pasender, Patrick-HC et 13 invités
Toutes les solutions de traitement du signal : différentes méthodes, matériel et logiciel, mise en œuvre...
.
- indien29
- Messages: 10531
- Inscription Forum: 05 Nov 2017 17:38
- Localisation: Paris - Bretagne 29
Tiens, l’indien a oublié qu’il avait réservé des espaces pour satisfaire sa fièvre d’écriture 

- Bachibousouk
- Pro-Divers

- Messages: 2433
- Inscription Forum: 06 Juin 2009 13:25
- Localisation: Besançon
Pour résumer, la distance critique peut être estimée à l’aide de la relation: dc=√(AQ/50) ce qui suppose de pouvoir :
- Mesurer le Tr de sa pièce pour en déduire A=0,16V/Tr
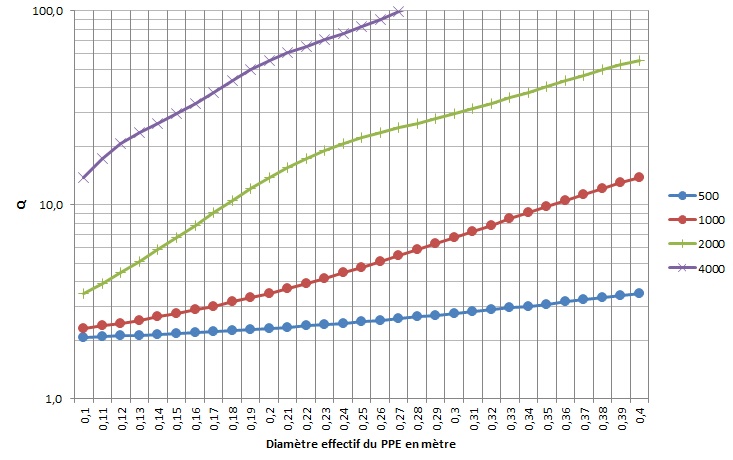
- Estimer le facteur de directivité Q de son enceinte ou de son HP
Pour établir cette formule, il a été considéré deux champs sonores:
- le champ direct, qui vaut dans l’axe d’une source directive: L=Lw-11-20 log(r)+10 log (Q)
- le champ diffus qui ne dépend que de l’absorption de la salle A (ou constante de salle): L’=Lw+6-10log(A)
Avec Lw le niveau de puissance de la source, exprimé en dB.
À la distance critique, on égalise les niveaux de pression quadratique, L=L’ ce qui amène après transformation à la relation simple dc=√(AQ/50).
Une approche rapide pour un volume de 50 m3, un Tr de 0,5 s, un HP à radiation directe de 17 cm (dont Q=2,2 à 500 Hz), donne une distance critique de 0,84 m à 500 Hz ! Au-delà de 3 fois la distance critique le champ diffus domine de plus 10 dB le champ direct ! Autant dire que trois fois la distance critique, appelé aussi distance hypercritique, est l'ultime limite à ne pas dépasser en acoustique des salles, surtout quand l'auditeur a payé sa place. En conséquence, dans son séjour, il vaut mieux être proche de ces enceintes.



Bachi
- Mesurer le Tr de sa pièce pour en déduire A=0,16V/Tr
- Estimer le facteur de directivité Q de son enceinte ou de son HP
Pour établir cette formule, il a été considéré deux champs sonores:
- le champ direct, qui vaut dans l’axe d’une source directive: L=Lw-11-20 log(r)+10 log (Q)
- le champ diffus qui ne dépend que de l’absorption de la salle A (ou constante de salle): L’=Lw+6-10log(A)
Avec Lw le niveau de puissance de la source, exprimé en dB.
À la distance critique, on égalise les niveaux de pression quadratique, L=L’ ce qui amène après transformation à la relation simple dc=√(AQ/50).
Une approche rapide pour un volume de 50 m3, un Tr de 0,5 s, un HP à radiation directe de 17 cm (dont Q=2,2 à 500 Hz), donne une distance critique de 0,84 m à 500 Hz ! Au-delà de 3 fois la distance critique le champ diffus domine de plus 10 dB le champ direct ! Autant dire que trois fois la distance critique, appelé aussi distance hypercritique, est l'ultime limite à ne pas dépasser en acoustique des salles, surtout quand l'auditeur a payé sa place. En conséquence, dans son séjour, il vaut mieux être proche de ces enceintes.
Bachi
Dernière édition par Bachibousouk le 02 Juil 2019 17:31, édité 3 fois.
- Bachibousouk
- Pro-Divers

- Messages: 2433
- Inscription Forum: 06 Juin 2009 13:25
- Localisation: Besançon
- Bachibousouk
- Pro-Divers

- Messages: 2433
- Inscription Forum: 06 Juin 2009 13:25
- Localisation: Besançon
La même chose mais pour un pavillon où alpha et béta représentent les angles d'ouverture à -6 dB
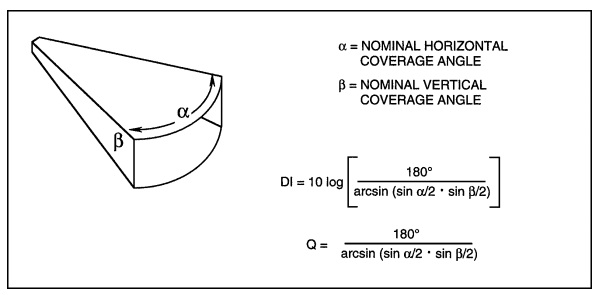
En pratique, il est fortement recommandé que le facteur de directivité du boomer et du pavillon soit du même ordre de grandeur, au moins à la fréquence de croisement du filtre.
Par exemple, un 30 cm coupé à 1000 Hz associé à un pavillon 60 x 120°, va bien
Mais si on opte pour une directivité verticale ressérée, ça se complique un peu.



Bachi


En pratique, il est fortement recommandé que le facteur de directivité du boomer et du pavillon soit du même ordre de grandeur, au moins à la fréquence de croisement du filtre.
Par exemple, un 30 cm coupé à 1000 Hz associé à un pavillon 60 x 120°, va bien
Mais si on opte pour une directivité verticale ressérée, ça se complique un peu.
Bachi
- Bachibousouk
- Pro-Divers

- Messages: 2433
- Inscription Forum: 06 Juin 2009 13:25
- Localisation: Besançon
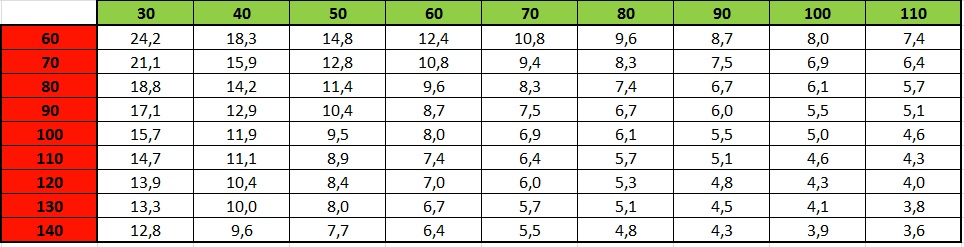
Les angles annoncés sur les pavillons à profils asymétriques sont très peu tenu aux fréquences de coupure.
Ne pas se fier aux données constructeurs qui annoncent 90x40° par exemple ou prendre soin de bien noter pour quelles fréquences cet angle est tenu et avec quel niveau.
J'ai repris cette formule qui est très pratique sur la doc JBL
Si la doc du pavillon dispose d'un diagramme polaire, on peut estimer l'indice de directivité à partir de cette formule pour plusieurs fréquences.
Ne pas se fier aux données constructeurs qui annoncent 90x40° par exemple ou prendre soin de bien noter pour quelles fréquences cet angle est tenu et avec quel niveau.
J'ai repris cette formule qui est très pratique sur la doc JBL
Si la doc du pavillon dispose d'un diagramme polaire, on peut estimer l'indice de directivité à partir de cette formule pour plusieurs fréquences.
La configuration dans mon profil
Salle dédiée Hifi/HC
Vous appréciez HCFR ? Le forum HCFR existe parce que les cotisations des membres de l'Association HCFR le financent.
- JIM
- Modérateur Installations

- Messages: 7166
- Inscription Forum: 19 Nov 2001 2:00
- Localisation: Toulouse
Merci JIM pour tes remarques opportunes.
Si on analyse succinctement le facteur de directivité d’un module de sonorisation, celui-là par exemple:

Le VRX 928 est équipé d’un boomer-médium de 200 mm coupé à 2 kHz, ce qui donne Q=14 à 2 kHz (angle d’ouverture 74 ° pour le piston plan).
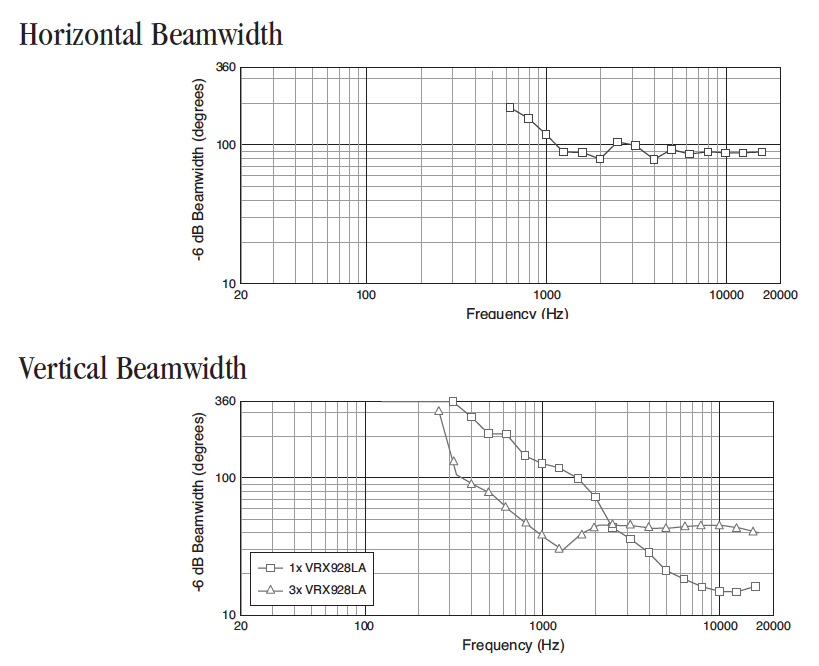
Les angles d’ouverture à -6 dB sont annoncés au-delà de 2 kHz, c’est-à-dire dans la zone fréquentielle de fonctionnement du pavillon, à 90 x 40 environ soit un facteur de directivité Q=13 d’après la formule de Molloy pour le pavillon.
JBL a soigné, autant que faire se peut, la cohérence de la directivité de ces éléments à la fréquence de raccordement du filtre



Bachi
Si on analyse succinctement le facteur de directivité d’un module de sonorisation, celui-là par exemple:

Le VRX 928 est équipé d’un boomer-médium de 200 mm coupé à 2 kHz, ce qui donne Q=14 à 2 kHz (angle d’ouverture 74 ° pour le piston plan).

Les angles d’ouverture à -6 dB sont annoncés au-delà de 2 kHz, c’est-à-dire dans la zone fréquentielle de fonctionnement du pavillon, à 90 x 40 environ soit un facteur de directivité Q=13 d’après la formule de Molloy pour le pavillon.
JBL a soigné, autant que faire se peut, la cohérence de la directivité de ces éléments à la fréquence de raccordement du filtre

Bachi
Dernière édition par Bachibousouk le 18 Juil 2019 14:48, édité 1 fois.
- Bachibousouk
- Pro-Divers

- Messages: 2433
- Inscription Forum: 06 Juin 2009 13:25
- Localisation: Besançon
Dans l’excellent ouvrage de Jacques Jouhaneau Notion élémentaires d’acoustique Électroacoustique l’auteur propose une méthode permettant le calcul du facteur de directivité global d’une enceinte deux voies:

Avec le Q global de l'enceinte, la distance critique se calcule à n’importe quelle fréquence à condition, bien sûr, de connaître le facteur de directivité que chacun des haut-parleurs, la fréquence de coupure et la pente du filtre que l’on suppose symétrique dans le cas présent.
Tout ça pour ça



Bachi

Avec le Q global de l'enceinte, la distance critique se calcule à n’importe quelle fréquence à condition, bien sûr, de connaître le facteur de directivité que chacun des haut-parleurs, la fréquence de coupure et la pente du filtre que l’on suppose symétrique dans le cas présent.
Tout ça pour ça
Bachi
- Bachibousouk
- Pro-Divers

- Messages: 2433
- Inscription Forum: 06 Juin 2009 13:25
- Localisation: Besançon
Pour illustrer ces relations, supposons une enceinte assez répandue dans le monde audiophile, constituée:
- d’un boomer de 15 pouces (diamètre effectif 34 cm)
- d'un pavillon TH40001 (90 x 40 °)
Le filtre est un 18 dB/oct avec une fréquence de coupure de 650 Hz (vue sur HCFR).
On souhaite connaître le facteur de directivité à 1000 Hz, par exemple.
Boomer Q1=9 à 1000 Hz
La formule de Molloy donne pour le pavillon Q2=13
Le filtre est du 3e ordre donc N=3
Avec fc=750 Hz, f=1000 Hz et N=3, le coef alpha vaut 1,9
En calculant le Q global, en optant pour un modèle non corrélé, on trouve au final:
Q=11,6 qui est le facteur de directivité de l’enceinte (boomer + pavillon) à la fréquence de 1000 Hz.
Maintenant si la fréquence est bien plus grande que 650 Hz, le facteur de directivité de l'enceinte sera très proche de celui du pavillon c'est-à-dire 13. Dans ce cas, les calculs sont inutiles.
Ça peut aider pour l’estimation de la distance critique.



Bachi
- d’un boomer de 15 pouces (diamètre effectif 34 cm)
- d'un pavillon TH40001 (90 x 40 °)
Le filtre est un 18 dB/oct avec une fréquence de coupure de 650 Hz (vue sur HCFR).
On souhaite connaître le facteur de directivité à 1000 Hz, par exemple.
Boomer Q1=9 à 1000 Hz
La formule de Molloy donne pour le pavillon Q2=13
Le filtre est du 3e ordre donc N=3
Avec fc=750 Hz, f=1000 Hz et N=3, le coef alpha vaut 1,9
En calculant le Q global, en optant pour un modèle non corrélé, on trouve au final:
Q=11,6 qui est le facteur de directivité de l’enceinte (boomer + pavillon) à la fréquence de 1000 Hz.
Maintenant si la fréquence est bien plus grande que 650 Hz, le facteur de directivité de l'enceinte sera très proche de celui du pavillon c'est-à-dire 13. Dans ce cas, les calculs sont inutiles.
Ça peut aider pour l’estimation de la distance critique.
Bachi
- Bachibousouk
- Pro-Divers

- Messages: 2433
- Inscription Forum: 06 Juin 2009 13:25
- Localisation: Besançon
Bonjour Bachi,
Merci pour ton temps sur ce post et pour ton analyse.
Pour ceux qui comme moi, ne sont pas bon en math, pourrais tu nous préparer une feuille Excel dans laquelle on rentrerait d'un coté le RT (à condition de pouvoir le définir) et de l'autre le Q de l'enceinte ?
Merci à toi !
Merci pour ton temps sur ce post et pour ton analyse.
Pour ceux qui comme moi, ne sont pas bon en math, pourrais tu nous préparer une feuille Excel dans laquelle on rentrerait d'un coté le RT (à condition de pouvoir le définir) et de l'autre le Q de l'enceinte ?
Merci à toi !
- indien29
- Messages: 10531
- Inscription Forum: 05 Nov 2017 17:38
- Localisation: Paris - Bretagne 29
Inutile d’être bon en maths, il faut juste savoir calculer.
Jean Fourcade, sur le forum d’à côté, a conçu un modèle assez similaire à l’idée initiale de JIM, c’est-à-dire mesurer la décroissance du son pour en déduire la distance critique. L’auteur de la feuille Excel à cependant une approche calculatoire plus rigoureuse. C’est donc l’occasion de tester le modèle de monsieur Fourcade avec les mesurages réalisés en octobre 2018 dans une pièce de 255 m3 (tableau figurant dans la page précédente).
La feuille de calcul de M. Fourcade a préalablement été complété est ci-dessous:
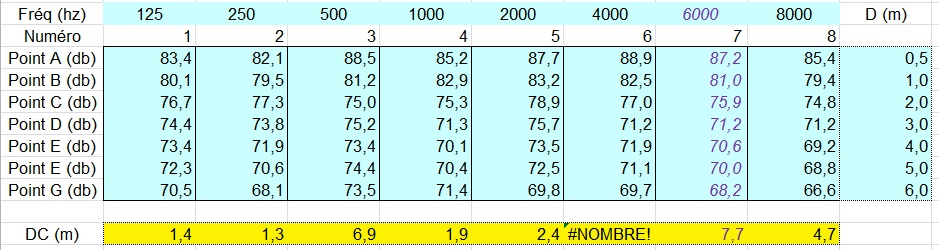
Ne pas tenir compte de la colonne de 6000 Hz incrémentée n’importe comment.
Le Tr mesuré sur bruit impulsionnel est assez linéaire dans cette pièce puisqu’il varie de 0,35 seconde à 125 Hz à 0,32 seconde à 4 kHz. Le facteur de directivité Q de l’enceinte (Mipro MA 708), non documenté, devrait croître avec la fréquence. En conséquence, la distance critique devrait également croître avec la fréquence. Or ce n’est pas le cas !
Néanmoins, si je calcule la distance critique à 125 Hz où je suis certain que le boomer a un comportement quasi omnidirectionnel, je trouve une distance critique de 1,53 m (Tr=0,35 s; Q=1) pour 1,4 m avec le modèle «Fourcade». C’est cohérent.
A contrario, à 500 Hz la valeur annoncée dans le tableur de 6,9 m est dans les choux car la formule usuelle donne 2,3 m (T=0,34 s; Q=2,3). Cela s’explique par des niveaux sonores à 500 Hz très «sales » avec une pente initiale de 7 dB/oct, 6 dB/oct et 0 dB/oct (mesurage en milieu domestique avec réflexion sur de nombreux objets) !!! Évidemment, plus les niveaux mesurés seront proches de la courbe de décroissance théorique du formalisme de Sabine plus la distance critique estimée avec la feuille de Jean Fourcade sera fiable. La méthode sera d’autant plus précise que les mesures seront soignées. Bravo monsieur Fourcade, vous avez mis là un excellent outil de calcul à la portée de tous.



Bachi
Jean Fourcade, sur le forum d’à côté, a conçu un modèle assez similaire à l’idée initiale de JIM, c’est-à-dire mesurer la décroissance du son pour en déduire la distance critique. L’auteur de la feuille Excel à cependant une approche calculatoire plus rigoureuse. C’est donc l’occasion de tester le modèle de monsieur Fourcade avec les mesurages réalisés en octobre 2018 dans une pièce de 255 m3 (tableau figurant dans la page précédente).
La feuille de calcul de M. Fourcade a préalablement été complété est ci-dessous:

Ne pas tenir compte de la colonne de 6000 Hz incrémentée n’importe comment.
Le Tr mesuré sur bruit impulsionnel est assez linéaire dans cette pièce puisqu’il varie de 0,35 seconde à 125 Hz à 0,32 seconde à 4 kHz. Le facteur de directivité Q de l’enceinte (Mipro MA 708), non documenté, devrait croître avec la fréquence. En conséquence, la distance critique devrait également croître avec la fréquence. Or ce n’est pas le cas !
Néanmoins, si je calcule la distance critique à 125 Hz où je suis certain que le boomer a un comportement quasi omnidirectionnel, je trouve une distance critique de 1,53 m (Tr=0,35 s; Q=1) pour 1,4 m avec le modèle «Fourcade». C’est cohérent.
A contrario, à 500 Hz la valeur annoncée dans le tableur de 6,9 m est dans les choux car la formule usuelle donne 2,3 m (T=0,34 s; Q=2,3). Cela s’explique par des niveaux sonores à 500 Hz très «sales » avec une pente initiale de 7 dB/oct, 6 dB/oct et 0 dB/oct (mesurage en milieu domestique avec réflexion sur de nombreux objets) !!! Évidemment, plus les niveaux mesurés seront proches de la courbe de décroissance théorique du formalisme de Sabine plus la distance critique estimée avec la feuille de Jean Fourcade sera fiable. La méthode sera d’autant plus précise que les mesures seront soignées. Bravo monsieur Fourcade, vous avez mis là un excellent outil de calcul à la portée de tous.
Bachi
- Bachibousouk
- Pro-Divers

- Messages: 2433
- Inscription Forum: 06 Juin 2009 13:25
- Localisation: Besançon
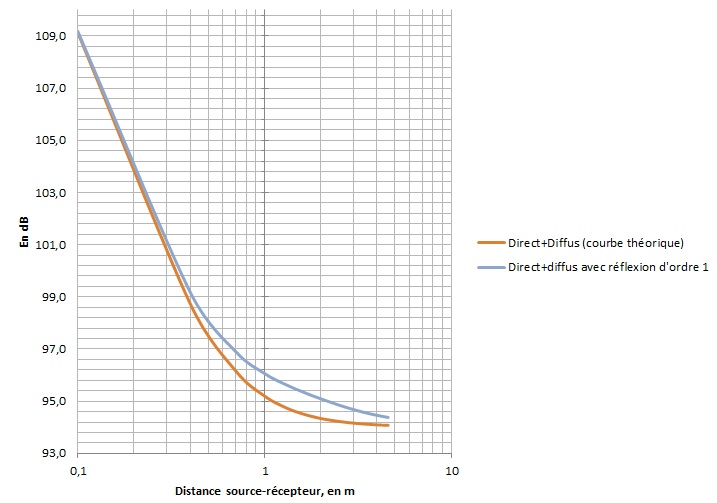
Le graphique ci-dessous montre l’incidence des réflexions d’ordre 1 dans une pièce de dimensions 6 x 4 x 2,5, source omni disposée à 0,5 m des murs (triangle d’écoute classique). Le Tr Sabine est dans le cas présent de 0,61 s.
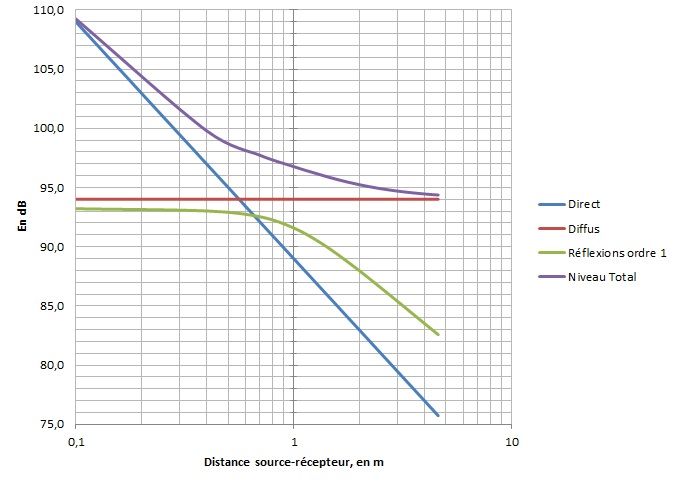
Le niveau des six réflexions primaires (phases considérées aléatoires) n’est pas à négliger ! Mais la source est omnidirectionnelle. Le résultat avec une enceinte directive serait sans doute moins spectaculaire.
Le poids relatif de chacune des réflexions, pour info:
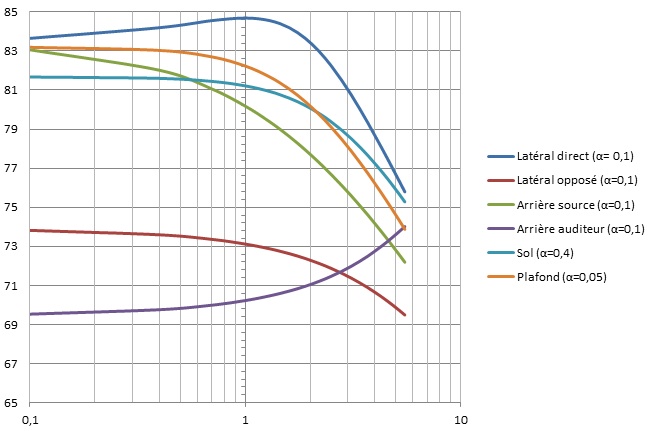



Bachi

Le niveau des six réflexions primaires (phases considérées aléatoires) n’est pas à négliger ! Mais la source est omnidirectionnelle. Le résultat avec une enceinte directive serait sans doute moins spectaculaire.
Le poids relatif de chacune des réflexions, pour info:

Bachi
Dernière édition par Bachibousouk le 17 Mar 2021 18:52, édité 1 fois.
- Bachibousouk
- Pro-Divers

- Messages: 2433
- Inscription Forum: 06 Juin 2009 13:25
- Localisation: Besançon
- Bachibousouk
- Pro-Divers

- Messages: 2433
- Inscription Forum: 06 Juin 2009 13:25
- Localisation: Besançon
- tcli
- Messages: 4091
- Inscription Forum: 23 Nov 2009 22:40
- Localisation: Encore plus à l'ouest qu'avant
|
Retourner vers Correction active et logiciels de mesure
|