Loi de Rayleigh-Réflexion/diffusion

[Bachibousouk]

La diffusion du son est un sujet très rarement abordée dans les ouvrages acoustiques de langue française. Jouhaneau se contente dans le très bon acoustique des salles et sonorisation d’en donner la définition en quelque ligne, alors que Mario Rossi dans Audio est à peine plus loquace avec trois à quatre pages consacrées à la diffusion sur un livre qui en compte plus de 700.

Compte tenu de la difficulté de fabriquer pour un amateur des panneaux de Schroeder, il est peut être judicieux comme l’évoquait Emanuelle Piat dans un autre sujet, de détourner des objets et des matériaux déjà existants pour les utiliser comme des diffuseurs.

Mario Rossi dans son livre introduit la loi de Rayleigh qui permet d’évaluer sommairement si une surface irrégulière diffuse ou réfléchit suivant les lois de l’acoustique spéculaire. Un modèle qui peut s’avérer précieux à l’amateur pour évaluer le caractère diffusant d’une surface irrégulière.

Le principe est le suivant, je site Rossi:
Soit deux rayons incidents, le premier se réfléchissant au sommet d’une aspérité, le second en un creux: lorsque leur différence de trajet aux points de réflexion est inférieure à un huitième de la longueur d’onde, on considère que les rayons réfléchis interfèrent constructivement, si elle est supérieure, destructivement.



On caractérise alors cette surface de réflexion par le nombre de Rayleigh R

R=2kh sinß

Si R est assez petit il y a réflexion, et si R>1 alors il y a diffusion.

ß étant l’angle d’incidence
k le nombre d’onde (k=2πf/c)
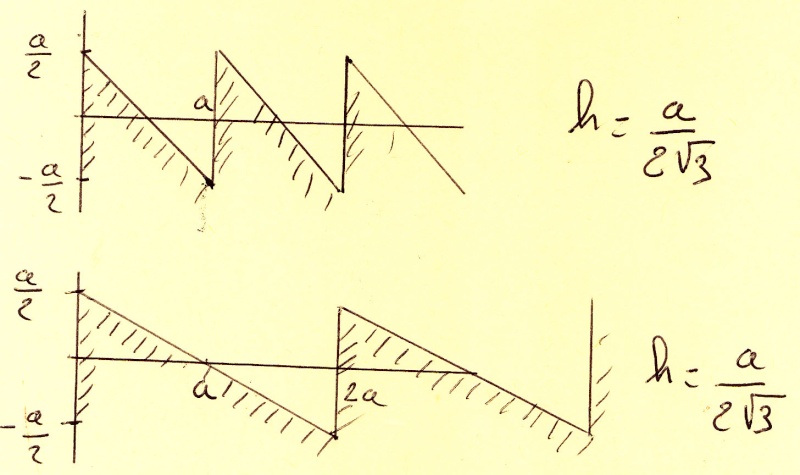
et h valeur efficace de la hauteur par rapport à la surface moyenne, représentant l’écart quadratique moyen de la hauteur des aspérités par rapport au plan moyen.
http://fr.wikipedia.org/wiki/Valeur_efficace" onclick="window.open(this.href);return false;

Le calcul de h peut s’avérer délicat, mais pour les surfaces usuelles (dents de scie, créneau et sinusoïde), il est relativement aisé. J’indique ici les valeurs de h pour des profondeurs valant toujours a.



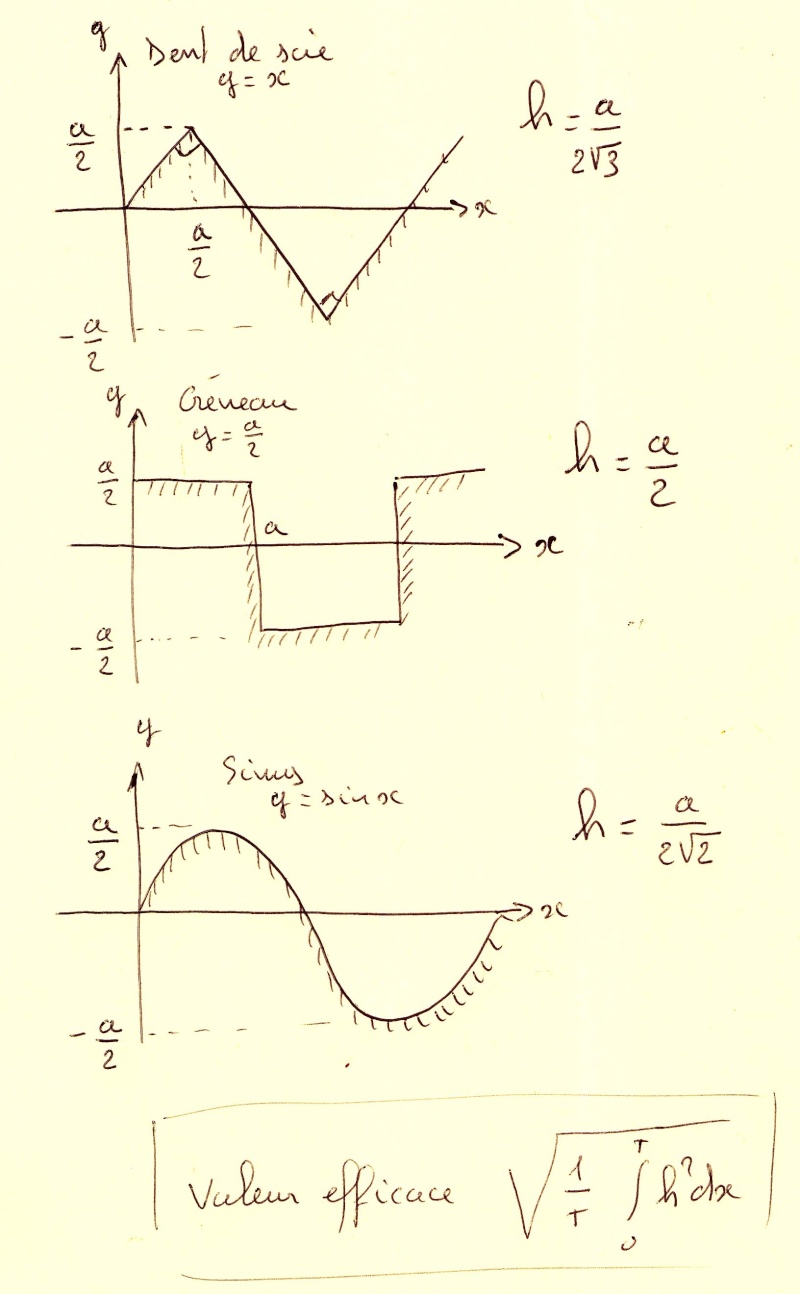
A vos calculettes
Pour en discuter.

Bachi

[ohl]

En reprenant ces calculs dans un cas typique (et favorable) avec h=a/2, on arrive au résultat suivant : pour a=50cm, f=150Hz
Dans une pièce d'habitation, la fréquence de Schroeder qui définit approximativement la limite du comportement modal se situe entre 120 et 180Hz. Il est souvent conseillé de garder une certaine homogénéité au-dessus de cette fréquence : ce qui implique donc l'utilisation de diffuseurs ayant au moins 50cm de profondeur.
Ce qui implique que les diffuseurs fait à partir de casiers à CD Ikea aléatoirement remplis, c'est un peu juste ! Des casiers à bouteilles sont sans doute plus équilibrés spectralement (surtout les casiers pour magnums)

[bss]

+ 1000

[Gort'h]

Bonjour à tous

Franchement chapeau à vous tous qui lançez des fils comme celui là.
C'est à la fois intéressant, instructif et je suis épaté par les connaissances de certains.

Ce calcul peut être utilisé donc pour vérifier comment nos "meubles" diffusent ou pas c'est ça?
Mais cela s'avére compliqué a moins de ramener à un modèle usuel qui sera moins précis (style dent de scie ou autre)?

En tous cas je lis ces posts avec curiosité et enthousiasme. Continuez!

A+

Gort'h

[Bachibousouk]

Merci Gort'h pour cet encouragement

Ohl, vous êtes un briseur de rêve et un pourfendeur d’espoir pour tous les détourneurs d’objets de la planète audio, mais Rayleigh est implacable et vous donne évidemment raison

Je me suis quand même amusé à calculer la fréquence de diffusion* pour les structures envisagées plus haut, en prenant arbitrairement un angle d’incidence ß de 45°.
Pour une profondeur du motif a de 10 cm, on trouve:

Dent de scie: f= 1330 Hz
Créneau: f= 750 Hz
Sinusoïde : f= 1080 Hz

Ces résultats présentent un aspect pratique intéressant puisque la fréquence de diffusion f est inversement proportionnelle à la profondeur a du motif.

Exemples :
- Pour un motif en dent de scie de 20 cm de profondeur, soit 2 x 10 cm, la fréquence de diffusion est alors de 1330/2=665 Hz

- De même, pour un motif en créneau de 50 cm de profondeur, soit 5 x 10 cm, la fréquence de diffusion est alors de 750/5=150 Hz, qui correspond heureusement au résultat indiqué par Ohl.

Dorénavant, nul internaute ne pourra ignorer la limite entre réflexion et diffusion d’une surface irrégulière, et les achats chez Ikéa seront maintenant grandement facilités

Bachi
* Fréquence à partir de laquelle il y a diffusion.

[Bachibousouk]

Les structures en dents de scie sont assez défavorisées d’après la loi de Rayleigh avec une valeur efficace de la hauteur h assez faible par rapport à une structure créneau . Pourtant par leur aspect visuel, elles sont assez engageantes.



Je me suis alors interrogé sur la possibilité d’obtenir une surface en dents de scie pressentant une meilleure valeur efficace de la hauteur h, pour diffuser davantage à profondeur égale, en calculant h pour deux nouvelles structures en dents de scie.



Sauf erreur de ma part, on retrouve encore une fois la même valeur de h avec a/(2√3).
Ça, c’est moche, mais je n’ai pas encore fait le tour de la question

Bachi

[Igor Kirkwood]

Notons que les revêtements acoustiques absorbants sont souvent de type alvéolaires (donc absorbsion + un peu de diffusion).

Les calculs donnés ici permetent de préciser l'effet diffusant: utile, merci.

Igor Kirkwood

[wuwei]

Comment peut-on considérer une surface de type crépi irrégulier d'intérieur ?

[ohl]

Comment peut-on considérer une surface de type crépi irrégulier d'intérieur ?

du point de vue d'une chauve-souris, c'est un excellent diffuseur

plus sérieusement,

Sauf erreur de ma part, on retrouve encore une fois la même valeur de h avec a/(2√3).
Ça, c’est moche, mais je n’ai pas encore fait le tour de la question

cherchons les limites de validité de cette loi de Rayleigh

[Bachibousouk]

Comment peut-on considérer une surface de type crépi irrégulier d'intérieur ?

du point de vue d'une chauve-souris, c'est un excellent diffuseur

C'est à dire wuwei qu'il y a diffusion à partir de 20 000 Hz environ

cherchons les limites de validité de cette loi de Rayleigh

Je cherche mais pour l'instant je séche un peu même si j’ai cru comprendre que Rayleigh était initialement lié à la diffusion des particules ou des ondes électromagnétiques. Pas forcement adaptable aux "dimensions sonores"

Bachi

[wuwei]

Je n'entend pratiquement plus au-dela de 14kHz



Peut-être ceci ? plus joli que les diffuseurs..

[alpacou]

Joli carrelage anywé.

[wuwei]

Non je vois plus ça pour le sol



C'est loin des équations de Rayleigh, désolé pour le HS

[frgirard]

Je n'entend pratiquement plus au-dela de 14kHz



Peut-être ceci ? plus joli que les diffuseurs..

moi c'est 11/12kHz. une soprano c'est 1Khz, ça laisse encore de la marge.

Francois

[Bachibousouk]

On lit souvent qu’un objet diffuse une onde si les dimensions de son motif sont du même ordre de grandeur que la longueur d’onde du signal. Autrement dit, si une onde à une longueur très grande ou très petite devant les dimensions du motif il y aurait réflexion spéculaire.
Par exemple, dans le cours d’acoustique des salles de l’école d’architecture nationale de Grenoble, un schéma indique qu’une structure en dents de scie de périodicité 30 cm ne diffuserait que les ondes dont les fréquences sont comprises entre 300 et 1000 Hz.

http://www.grenoble.archi.fr/enseigneme ... stique.pdf" onclick="window.open(this.href);return false;

Or, cette règle est en contradiction avec la loi de Rayleigh qui ne fixe pas de limite haute à la diffusion. Lorsque la longueur d’onde devient très petite devant la dimension du motif, il continue à y avoir diffusion.
La loi dit même que l’amplitude du coefficient de réflexion est réduite, par rapport au dioptre plan lisse, d’un coefficient
X=exp(-2R^2).
Cette valeur du coefficient X tend très vite vers zéro lorsque R augmente.

Concrètement, pour une surface «sinus 2D» déjà évoquer plus haut de profondeur a=10 cm, diffusion théorique à partir de 1080 Hz sous 45°, on trouve:

à 279 Hz R=0,25 X=0,88 (réflexion)
à 540 Hz R=0,5 X=0,61 (réflexion)
à 1080 Hz R= 1 X=0,14 (diffusion)
à 2160 Hz R=2 X=0,0003 (diffusion «totale»)

Il apparaît, selon la loi de Rayleigh, que lorsque la longueur d’onde devient petite devant les dimensions du motif, la diffusion devient parfaite.

Le document très intéressant du CSTB téléchargeable ci-dessous donne plutôt raison à la loi de Rayleigh. On peut y observer des courbes de coefficients tracées en fonction de la fréquence, de plusieurs surfaces, dont un sinus 2D.

http://www.cstb.fr/fileadmin/documents/ ... -OK_BD.pdf" onclick="window.open(this.href);return false;


Bachi